一道有趣的中学几何题（附Matlab画动图代码）

发表于 | 分类于

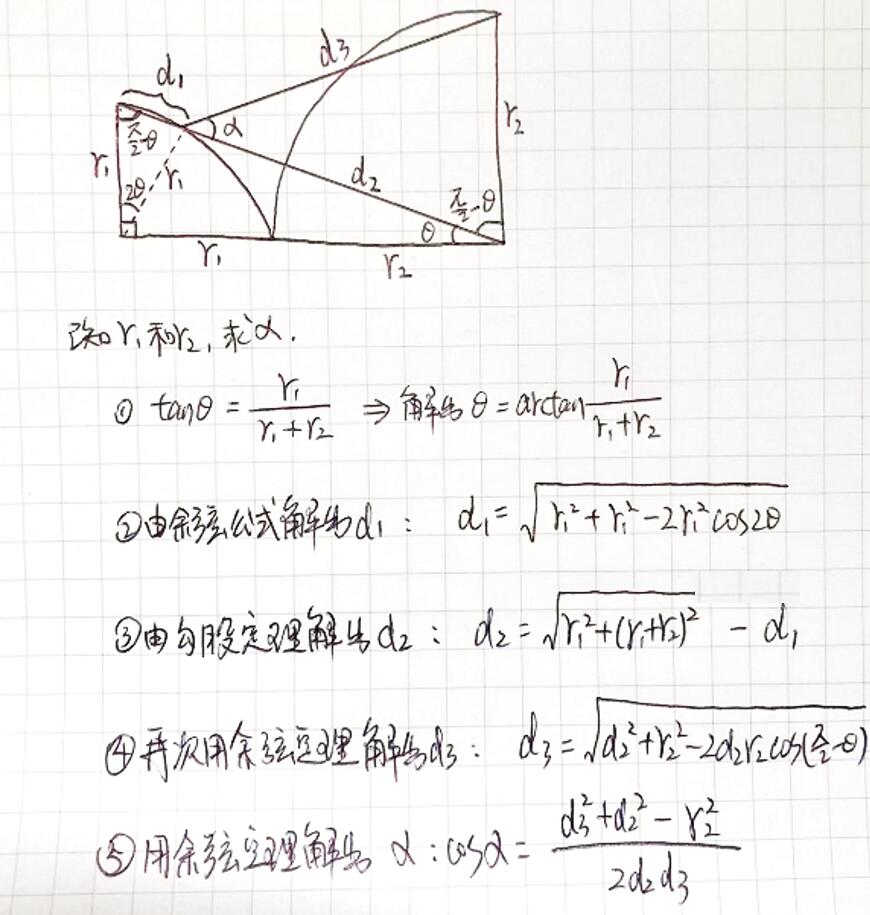
前段时间朋友给我发了一道中学的几何题让我做，题目是这样的：

Tips：题目中所要求的角度和两圆的半径无关。

暴力求解

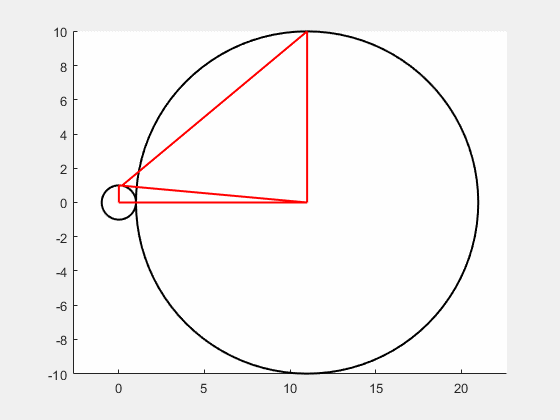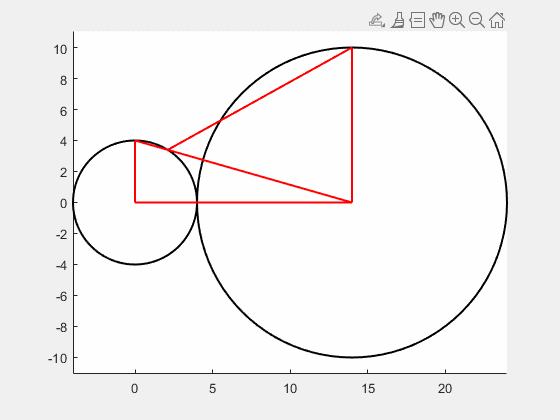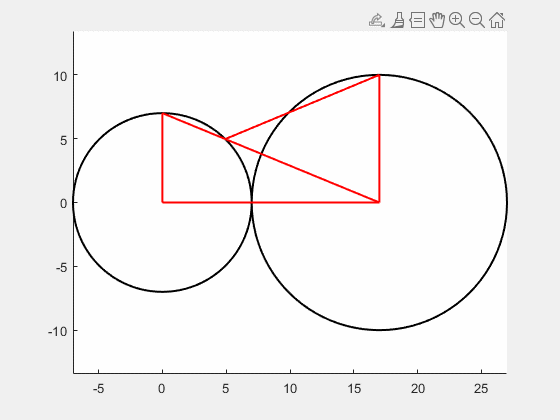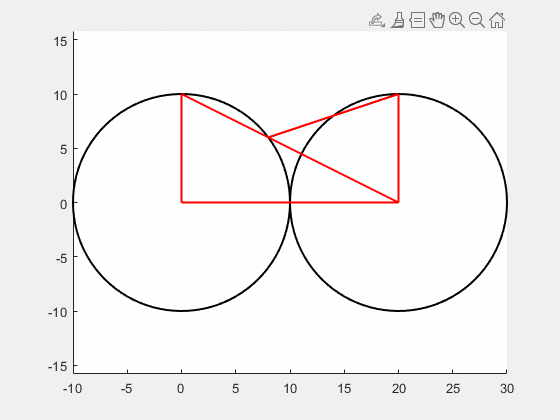
刚开始看到这道题的时候，我并不知道所要求的角度是不会随着两个圆的半径而变化的。

所以直接设两个圆的半径分别为R1，R2，通过用几次余弦定理和勾股定理就可以算出来了。

为了求出这个角度具体是多少，我写了一个Matlab程序，最后算出来是45°。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
clear;clc;
close all;

r1_range = 1:5; % 假设半径r1是变化的
r2 = 10; % 半径r2固定

alpha = zeros(length(r1_range), 1);
for i = 1:length(r1_range)
    r1 = r1_range(i);
    theta = atan(r1/(r1+r2));
    d1 = sqrt(2*r1*r1*(1-cos(2*theta)));
    d2 = sqrt(r1*r1 + (r1+r2)^2) - d1;
    d3 = sqrt(d2^2 + r2^2 - 2*d2*r2*cos(pi/2 - theta));
    alpha(i) = acos((d3^2 + d2^2 - r2^2)/(2*d2*d3))/pi*180;
end
plot(r1_range,alpha);

其实求解到这里就可以结束了，但我觉得这道题挺有意思，想画一个动图看一下半径变化过程中角度的变化，于是在网上找了一些关于如何在Matlab中画动图的方法，最后采用循环绘图的方法实现，效果如下图，代码见附录。

几何证明

后来朋友告诉我这道题有更简单的几何解法:)

1、设左/右边圆心为O1/O2，所求角顶点为A，两圆切点为B，左/右边的顶点为C/D，连接O1A，AB；
2、利用CABO1内角和360度，并且O1是圆心&CAB都在圆上，有两个等腰三角形（不一定全等）进而得到角相等，即BAO2为45度；
3、而角BDO2亦为45度，则有ABDO2共圆（判定：同侧共底三角形的顶角相等，则四点共圆）；
4、又由四点共圆性质，得角？=角DAO2=45度。

附录：Matlab代码

主函数：main.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
close all;
clc; clear;

r1_range = 1:0.1:20;
r2 = 10;

% 循环绘图
for i=1:length(r1_range);
    r1 = r1_range(i);
    cla;
    hold on;
    rectangle('Position',[-r1,-r1,r1*2,r1*2],'Curvature',[1,1],'linewidth',1.5);
    rectangle('Position',[ r1,-r2,r2*2,r2*2],'Curvature',[1,1],'linewidth',1.5);
    
    line1 = [0,0;(r1+r2),0];
    plot(line1(:,1),line1(:,2),'r','linewidth',1.5)
    
    line2 = [0,0;0,r1];
    plot(line2(:,1),line2(:,2),'r','linewidth',1.5)
    
    line3 = [r1+r2,0;r1+r2,r2];
    plot(line3(:,1),line3(:,2),'r','linewidth',1.5)
    
    line4 = [0,r1;r1+r2,0];
    plot(line4(:,1),line4(:,2),'r','linewidth',1.5)
    
    [x0, y0] = intersection_coordinate(r1, r2);
    line5 = [x0,y0;r1+r2,r2];
    plot(line5(:,1),line5(:,2),'r','linewidth',1.5)
    axis equal
    
    frame = getframe(gcf); % 截取影片帧
    imind = frame2im(frame); % 保存影片帧
    [imind, cm] = rgb2ind(imind,256);
    if i==1
        imwrite(imind,cm,'test.gif','gif', 'Loopcount',inf,'DelayTime',1e-4);
    else
        imwrite(imind,cm,'test.gif','gif','WriteMode','append','DelayTime',1e-4);
    end
end

直线和圆求交函数：intersection_coordinate.m

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function [x0, y0] = intersection_coordinate(r1, r2)
    % y = kx + b0
    k = -r1 / (r2+r1);
    b0 = r1*(r1+r2) / (r2+r1);
    a = 1 + k^2;
    b = 2*k*b0;
    c = b0^2 - r1^2;
    x1 = (-b + sqrt(b^2 - 4*a*c))/(2*a);
    x2 = (-b - sqrt(b^2 - 4*a*c))/(2*a);
    y1 = k*x1 + b0;
    y2 = k*x2 + b0;
    if(x1 < 0)
        x0 = x2; y0 = y2;
    else
        x0 = x1; y0 = y1;
    end
end