在有限元数值计算中,经常需要在四面体上进行面积分或体积分,积分方法通常选用的是高斯积分,在参考单元内定义一系列高斯积分点和与之对应的高斯积分权值。高斯积分策略分为两种,一种是将参考单元的积分点映射到实际单元中进行积分,另一种将实际单元上的积分映射到参考单元中进行计算,后者更为常用一些。本文主要描述了对于两个相邻四面体的交界面,当交界面左右两端定义的函数不相同时,两函数相乘在同一个面上的面积分计算方法。
问题描述
假设$f_1\left( \boldsymbol{x} \right)$和$f_2\left( \boldsymbol{x} \right)$分别为定义在两个相邻四面体内的函数,其表达式为:
现在我们需要求如下积分的结果:
其中$\partial \varOmega _k$表示在第 $k$个四面体上的边界面。
不失一般性,定义两个如下图所示的两个相邻四面体$\Omega _1$和$\Omega _2$:
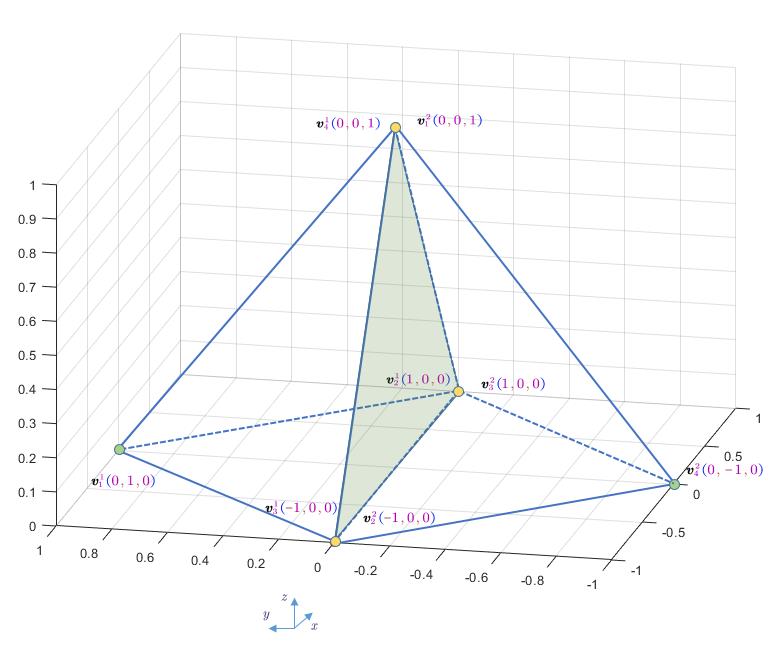
计算:两个四面体的交界面上的面积分。
方法1-直接积分
由于函数表达式已知,我们可以直接得到
直接运用高斯积分,原来的积分项可以简化为:
其中,$\boldsymbol{x}_k$为计算区域上的高斯积分点,$w_k$为对应高斯积分点的权。
计算结果为:-0.166667。
方法2-坐标映射积分
参考四面体
首先,在局部坐标系下定义如下图所示的参考四面体:
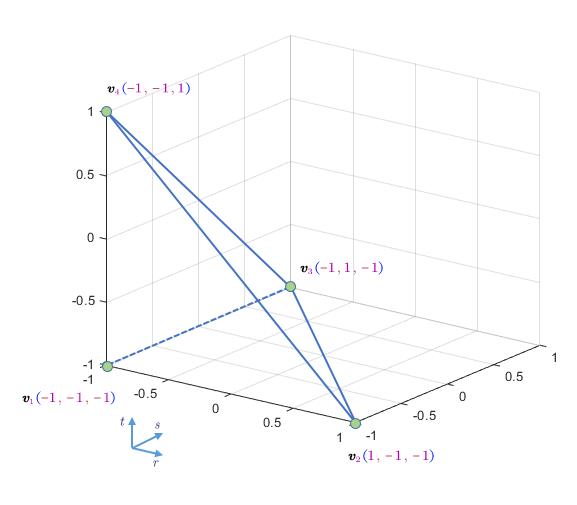
从任意四面体$\Omega _k$到参考四面体的映射关系为:
很容易检验上式只要代入在$\left(r,s,t\right)$坐标系下的参考四面体的四个顶点坐标,得到的就是实际四面体在$\left(x,y,z\right)$坐标系下的四个顶点坐标。
雅可比映射
从实际四面体到参考四面体的映射为线性映射,映射之间的雅可比系数满足如下关系:
其中$J$为雅可比矩阵行列式的值,可以通过映射的函数关系$\boldsymbol{x}=\varPsi \left( \boldsymbol{r} \right)$求出。
因此通过求雅可比矩阵的逆和左乘一个单元矩阵,容易就求出$r_x,r_y,r_z$等系数。
求导链法则
由于函数$f_2(\boldsymbol{x})$是定义在四面体$\Omega _2$上的函数,根据求导链法则可以得到:
根据上述的映射关系,有:
代入$\Omega _2$的四个顶点坐标,易得:
在参考四面体下的函数$f_2\left( \boldsymbol{r} \right)$可以表示为:
对于的偏导项分别为:
通过雅可比矩阵可以计算出系数:$r_y=1,s_y=1,t_y=-2.$
对积分而言,我们可以将其简化为:
其中面上的雅可比系数$J{f}^{k}$为实际面与映射面的面积之比。
积分点匹配
注意到$\Omega _1$在交界面上是映射到参考单元$(\boldsymbol{v_2,v_3,v_4})$构成的面,而$\Omega _2$是映射到$(\boldsymbol{v_2,v_3,v_4})$所构成的面。由于我们是预先在参考四面体上生成了高斯积分点,当想采用高斯积分来求解的时候,需要在两个面之间做一个高斯积分点匹配的过程。例如,如下图所示,在左边的四面体上交界面映射到的是参考单元的$(\boldsymbol{v_2,v_3,v_4})$面,右边四面体的交界面映射到的是参考单元的$(\boldsymbol{v_1,v_3,v_4})$面,实际交界面上的同一个点由左边的四面体映射到的是一个面上的 3 号积分点,而右边四面体映射到的是另一个面上的 5 号积分点。我们可以选择在两个面上的任意一个面做积分,只是不同面上的雅可比系数$J_{f}^{k}$有所不同。
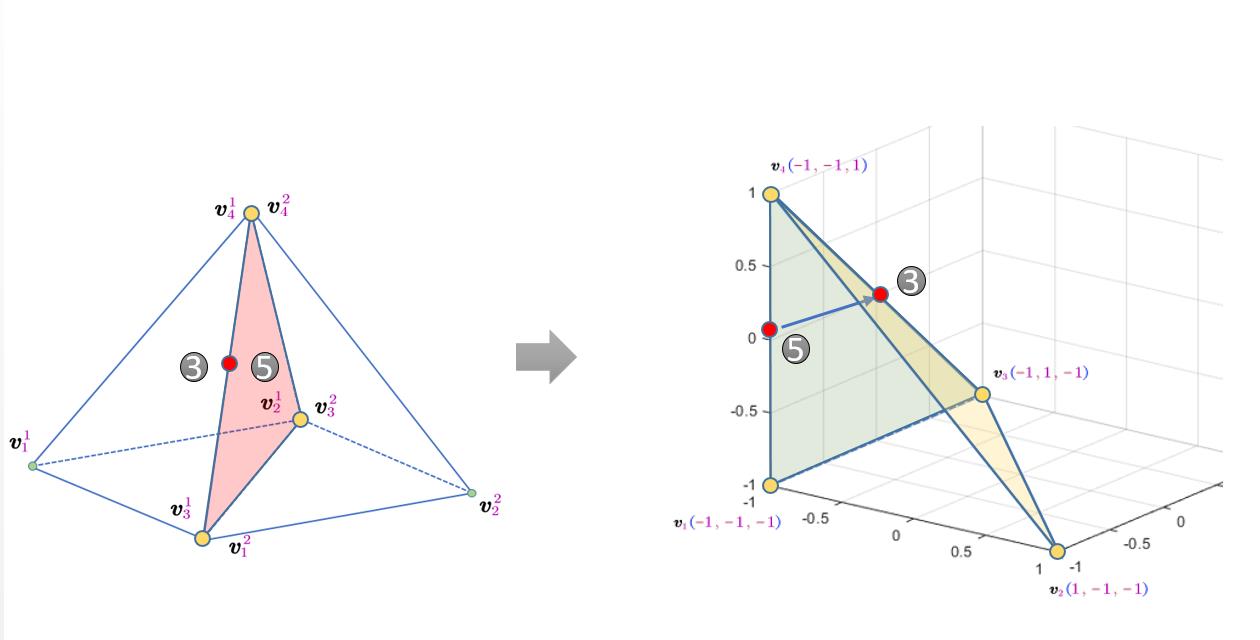
在本文中以第一个四面体$\Omega _1$在交界面映射到参考单元的 $(\boldsymbol{v_2,v_3,v_4})$ 面为积分面,对$\Omega _2$映射到第$(\boldsymbol{v_1,v_2,v_3})$面做高斯积分点匹配,结果如下图所示。
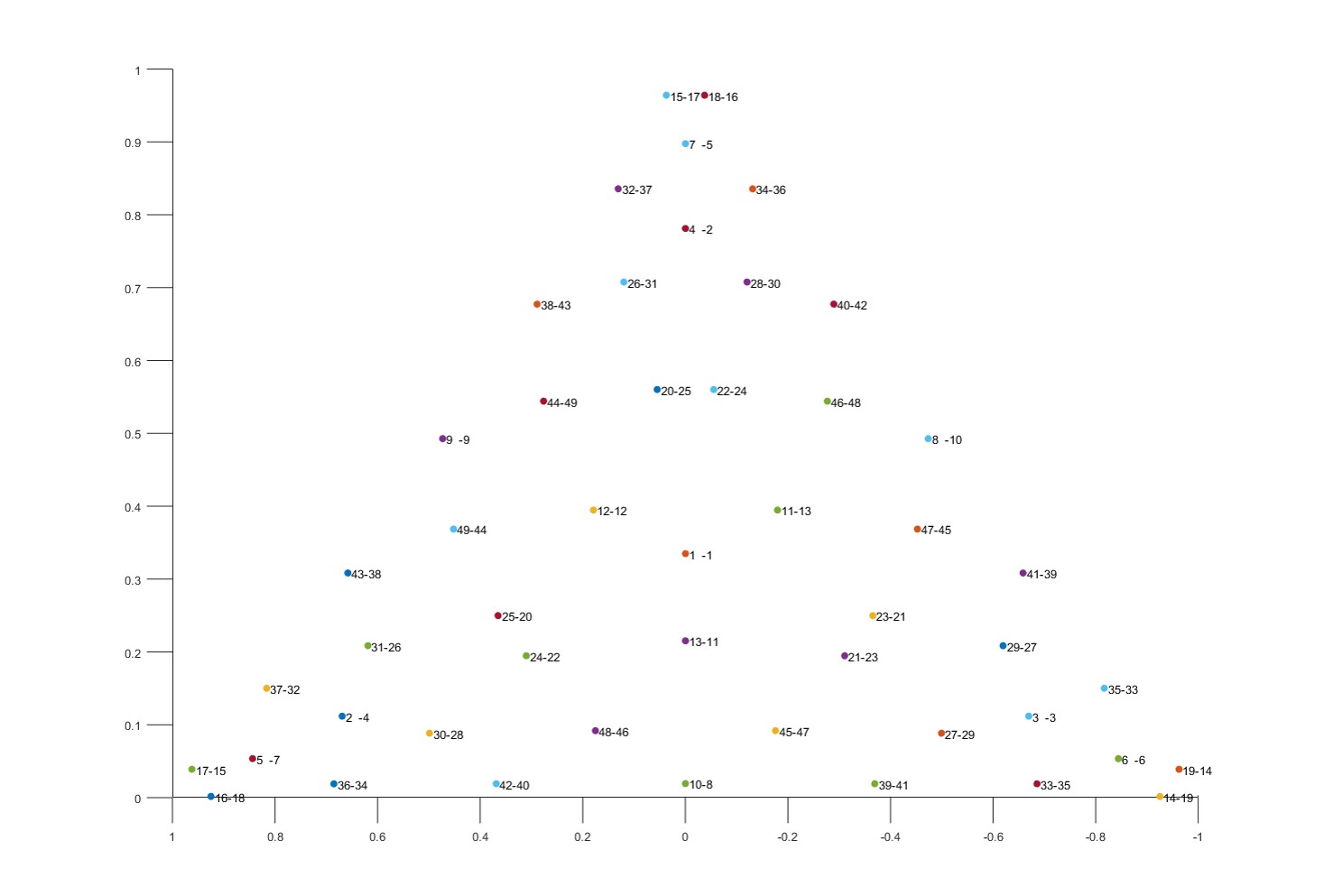
最后求解
通过求雅可比系数和建立高斯积分点匹配表,我们可以最后求解得到该面积分的值为−0.166667,和方案1是一致的。
总结
通过对比两种高斯积分方案,验证了参考四面体上进行积分映射可以得到实际四面体上的积分。这样做的好处是,在有限元算法中我们只需要存储一个参考四面体上的矩阵和一些与实际四面体相关的雅可比系数,而不需要对实际中每一个四面体都存矩阵,这样就实现了低存储的方案。